[Improving Deep Neural Networks: Hyperparameter Tuning, Regularization an Optimization] Practical Aspects of Deep Learning

✏️ Setting up your ML application

 

 Train/dev/test sets

 

 모델의 하이퍼파라미터(계층 수, 은닉 유닛 수, 학습률, 활성화 함수)을 정한 후 코드로 구현하고 훈련을 시켜본 후  값을 조금 변경해보면서 성능이 어떤 값을 가진 모델이 제일 좋은지 측정하여야 한다. 최적의 하이퍼파라미터는 한 번에 구하는 것이 거의 불가능하며 수차례 반복 과정을 거쳐야 한다. 가장 최적의 성능을 가진 모델을 찾았다고 해도 이것이 다른 작업/분야에도 똑같이 적용되는 것이 아니며 모든 모델을 설계할 때마다 이러한 작업을 반복해야한다. 

 

 이렇게 작업을 반복하며 모델의 성능을 측정하여야 하는데, 이때 필요한 것이 train/dev/test set이다. 이 set은 자료들의 집합을 의미하는데 각 집합마다의 목적이 다르다. 우선 training set은 설계한 모델을 학습시킬 때 사용하는 자료이고, dev set(=cross-validation set)는 어떤 모델이 가장 좋은 성능을 내는지 확인할 때 사용하는 자료다. 마지막으로 test set은 dev set으로 얻은 각 모델의 성능을 기반으로, 최적의 성능을 가진 모델(최종 모델)을 test set에 적용시켜 알고리즘의 최종 성능을 평가하는 것이다.

 

 자료가 있을 때 train/dev/test로 자료를 나누는 비율은 자료의 크기에 따라 달라진다. 예를 들어 10,000개 정도의 많지 않은 자료가 전부라 하면 60/20/20 비율로 적절히 나누고, 반대로 1,000,000개 정도로 자료가 아주 많다고 하면 98/1/1 비율 정도로 나누어 사용하면 된다. dev/test data는 어느 알고리즘을 가진 모델이 잘 작동하는지 빠르게 평가해야 하므로 엄청나게 많은 자료를 필요로 하진 않는다. 

 

 주의해야할 점을 dev set과 test set은 같은 곳으로부터 자료가 생성되어야 하는데, 예를 들어 <dev set은 사람이 직접 찍은 이미지, test set은 cctv가 찍은 이미지>처럼 다른 곳에서 자료가 생성되면 안된다. 참고로 test set은 필수 요소가 아닌데, test set의 목표는 unbiased estimate를 하는 것이므로 이게 필요 없으면 train/dev set만 있어도 괜찮다.

 

 

 

 Bias / Variance

 

 우선 어떤 분류기가 높은 bias, high variance를 가지는지 알아보자. 

 

 

 이 그림을 해석해보면 underfitting한 분류기는 높은 bias, overfitting한 분류기는 높은 variance를 가진다는 것을 알 수 있다. 정리하자면 bias와 variance는 train set error와 dev set error로 평가하는 것인데, 4가지 예시로 이를 설명하겠다. 

 

 ① 낮은 train set error, 높은 dev set error -> high variance

   - 이러한 경우는 모델이 train set에 오버피팅된 상태다. 이렇게 되면 모델의 성능은 높게 평가가 되었지만, 실제로 다른 data를 넣었을 때 분류를 잘 하지 못할 가능성이 높다. 이 경우는 "high variance"라고 할 수 있다.

  

 ② 높은 train set error, 비슷한 dev set error -> high bias

   - 이 예시는 모델의 학습은 잘되지 않았지만 일반화는 잘된 상태다. 이 모델은 train data에도 잘 맞지 않으므로 언더피팅되었다고 할 수 있다. "high bias".

 

 ③ 높은 train set error, 높은 dev set error -> high bias, high variance

   - 이 모델은 학습도 잘되지 않았고, 일반화도 잘되지 않은 최악의 상태다. 실제로는 train set에서 언더핏되었지만, dev set에 비하면 train set에 오버핏된 것처럼 보인다..(정말 최악). "high bias", "high variance"

 

 ④ 낮은 train set error, 낮은 dev set error -> low bias, low variance

   - 이 경우는 학습도 잘되었고, 일반화도 잘 된 최상의 상태다. "low bias", "low variance"

정확한 표현인진 모르겠지만 bias는 train set에서 학습이 잘되었는지로 판단하고, variance는 train set과 dev set error를 비교하여 일반화가 잘되었는지로 판단할 수 있는 것 같다.

 

 

 

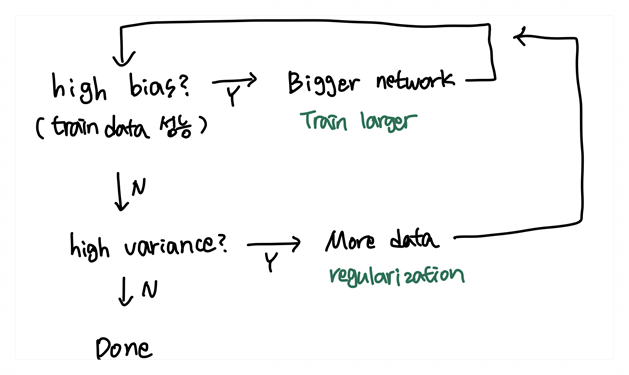
 Basic "recipe" for machine learning

 

 bias와 variance을 측정하여 모델의 성능을 어떻게 높일 수 있는지에 대해 알아보자. 원래는 "bias variance tradeoff"라고 해서 두 값이 서로 영향을 미치며 한 값이 낮아지면 다른 한 값이 올라가는 현상이 발생했는데, 큰 네트워크를 만들 수 있게 되면서 두 값은 서로 영향을 주지 않게 되었다.

 

 

 

 

✏️ Regularizing your neural network

 

 Regularization

 

 모델의 과적합을 막기 위해서는 regularization 과정이 필요하다. regularization은 비용 함수에 패널티를 주는 방법으로 가중치를 조절한다. 로지스틱 회귀와 신경망에 regularization을 적용하는 과정을 살펴보자.

 

[Logstic regression]

 

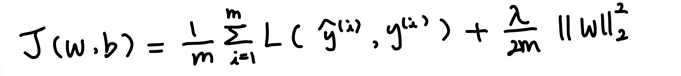
 위의 식은 로지스틱 회귀의 비용 함수에 regularization을 추가한 식이다. lambda는 정규화 매개변수이고, 여기서 사용한 regularization은 L2 regularization이다. 참고로 regularization은 w에만 적용을 하는데, w가 차원이 높아 대부분의 매개변수는 w에 속하기 때문이다. 

 regularization 방법에는 L2, L1 등 여러가지 방법이 있는데, 우선 L2와 L1에 대해 알아보겠다.

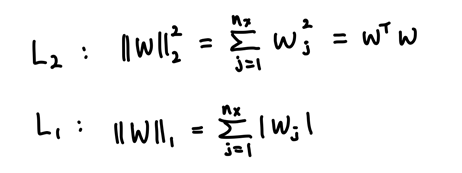
 위의 두 식은 각각 L2와 L1을 나타낸다. L2는 모든 유닛의 영향을 조금씩 줄이는 역할을 하지만, L1은 많은 w를 0으로 만들어 모델을 압축하는 효과를 낸다. 그렇기 때문에 L1는 거의 사용하지 않고, L2를 많이 사용한다. 

 

[Neural Network]

 

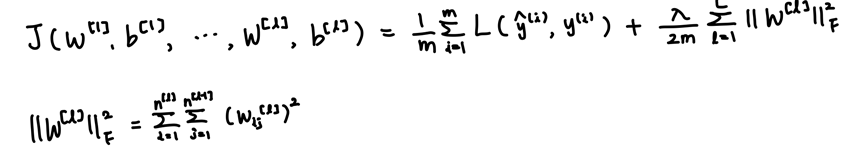
 위의 식은 신경망의 비용함수에서 regularization을 추가한 식이다. L2 정규화 방식을 추가하였고, 여기서는 ||W[l]||^2를 "Frobenius norm"이라고 부른다. 

 

 이처럼 regularization을 진행하면 dw에도 이 정규화의 영향이 미치게 된다. 

 기존의 backprop으로 계산한 dw에 regularization으로 인한 해당 식이 추가되는데, 이러한 이유로 경사하강을 진행할 때 w는 regularization을 하지 않았을 때보다 더 작아지는 효과를 가지게 된다. 그래서 L2 regularization을 "weight decay"라고도 한다. 

 

 

 

 Why regularization reduces overfitting

 

 regularization 과정이 오버피팅을 줄이는 원리에 대해 알아보자. 간단한 신경망을 그려 직관적으로 이해해보면 다음과 같은 그림으로 표현할 수 있다. 

 

 L2 regularization 과정을 거치면 전체적으로 w의 값들이 줄어든다. 따라서 많은 은닉 유닛의 영향이 줄어들게 되고, 일부 w들이 0에 가까운 값을 가지게 되었다 생각하면 신경망은 로지스틱 회귀에 더 가까운 신경망이 된다고 볼 수 있다.  이 과정을 통해 training data의 특징을 조금 덜 학습하게 되면서 오버피팅을 줄이는 것이다. 

 

 위의 내용을 tanh 그래프에 적용하여 조금 다른 방식으로 이해해 볼 수도 있다. L2 regularization으로 w 값(크기)이 줄어들고 따라서 z의 값이 원점에 가까운 값이 된다. tanh는 원점 지점에서 선형 함수와 비슷한 양상을 띄는데, 이 과정이 모든 layer에서 반복되면 전체 네트워크도 선형 네트워크가 되는 효과가 발생한다. 그러면 비선형 네트워크보다 조금 덜 복잡한 패턴을 학습하게 되며 오버피팅도 점점 줄어들 것이다. 

극단적으로 표현하면 이렇다는 것이지, 완전히 선형 함수를 쓰는 것이 아니기 때문에 진짜 선형 네트워크가 되진 않는다. 

 

 

 

 Dropout regularization

 

 dropout regularization은 각 layer에서 랜덤하게 유닛을 drop하는 방식이다. 그렇게 함으로써 training data의 특징을 조금 덜 학습하여 오버피팅을 줄인다. dropout 하는 방법은 각 layer마다 유닛을 drop할 확률을 정하고 drop이 확정된 유닛에는 0을 곱해 유닛의 영향을 없애는 것이다. 이를 식으로 표현하면 다음과 같다. 

 

# layer=3 가정
keep_prob=0.8	# drop 확률 0.2와 같은 의미
d3=np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob	#0.8보다 작으면 1, 아니면 0
a3=np.multiply(a3,d3)	# d3이 0인 유닛은 a3가 0이 됨
a3/=keep_prob	# 역드롭아웃 기술

 

 *역드롭아웃(Inverted dropout)

  - dropout을 적용하면 a[l] 요소의 20%가 0이 된다. 그러면 저절로 z와 a값도 평균적으로 20% 정도 줄어들게 되는데, 일관된 출력 크기를 위해 평균을 줄이지 않고자 역드롭아웃 기술을 적용한다. 역드롭아웃은 keep_prob을 a에 나누어 주면 된다. 

 

드롭 아웃을 적용하여 활성화 함수의 출력을 특정 확률로 무작위로 drop 하여 과적합을 방지하면서도, 훈련과 테스트 중에 네트워크의 활성화 값의 크기를 일관되게 유지할 수 있게 하는 것이다. 

 

 그리고 여기서 가장 중요한 점은 test 과정에서는 dropout을 하지 않고, keep prob으로 a의 스케일을 조정하지도 않는 것이다. 

 

 

 

 Other regularization methods

 

 L2, L1, dropout regularization 방식 외 다른 방법들에 대해 알아보자.

 

[Data augmentation]

이미지에 무작위적 왜곡과 변형을 주어 데이터를 증강시키는 방법이다. 이미지 뒤집기, 회적, 확대 등이 있다. 

 

[Early stopping]

 모델을 훈련할 때 반복 횟수가 늘어날수록 대개 w값은 점점 커진다. 따라서 훈련을 조기 종료시키는 방법으로 적당한 크기의 w를 선택하여 오버피팅을 막을 수 있다. 

 

 

 

✏️ Setting up your optimization problem

신경망의 훈련 속도를 높이는 방법들에 대해 알아보겠다. 

 

 Normalizing inputs

 

 input X의 평균과 분산으로 X를 normalize 시킨다.

normalization

 

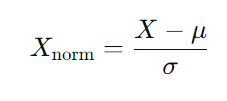
 normalize를 시키면 input 값들이 비슷한 범위를 가지게 되면서 경사 하강이 왔다갔다하는 현상 없이 잘 작동하게 된다. 아래는 이를 그림으로 표현한 자료다. 

 

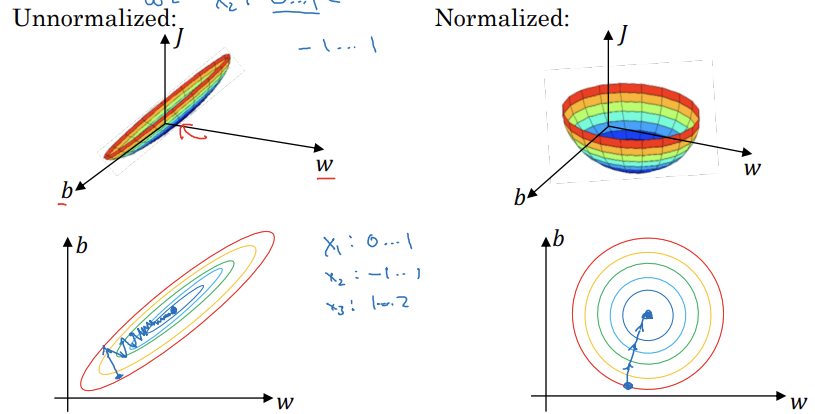
※ test data에도 train data에서 얻은 평균과 분산으로 정규화하면 된다. 

 

 

 

 Weight initialization for deep networks

 

 가중치는 값에 따라 모델을 훈련할수록 0으로 수렴하거나, 빨리 폭발하는 현상이 발생할 수 있다. 따라서 사용하는 활성화 함수에 따라 가중치 초기화를 잘 설정해서 이러한 현상들이 일어나지 않도록 방지해야한다. 

 

① 선형 활성화 함수

var(w): 1/n   (n: 뉴런으로 들어가는 입력 특징 수)

W[l]=np.random.randn(shape) * np.sqrt(1/n[l-1])

 

② Relu

var(w): 2/n    (n: 뉴런으로 들어가는 입력 특징 수)

W[l]=np.random.randn(shape) * np.sqrt(2/n[l-1])

 

③ tanh

  - xavier initialization

  W = np.random.randn(n_out, n_in) * np.sqrt(2 / (n_in + n_out))

  - other

   W = np.random.randn(n_out, n_in) * np.sqrt(2 /n[l-1] )

 

 

 

 Numerical approximation of gradients

 

 미분 계산이 옳게 되었는지 확인하기 위해 2가지 방법을 사용할 수 있다. 첫 번째 방법은 입력 변수의 값을 아주 조금 늘린 후 증가한 비율을 계산하는 것이다. 두 번째 방법은 입력 변수의 값을 양 옆으로 조금씩 줄이고 늘려서 조금 더 정확한 기울기 값을 계산하는 것이다. 

 

①

 

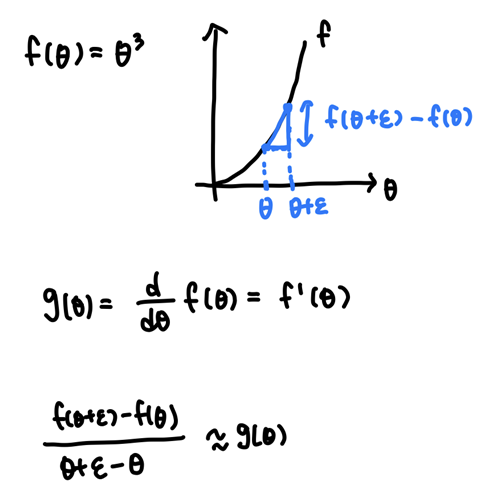
ex) ε=0.01

[(1.01)^3-(1^3)] / 0.01 = 3.0301 

g(1) = 3 

-> 3과 3.0301은 약 0.03 차이 

 

②

 

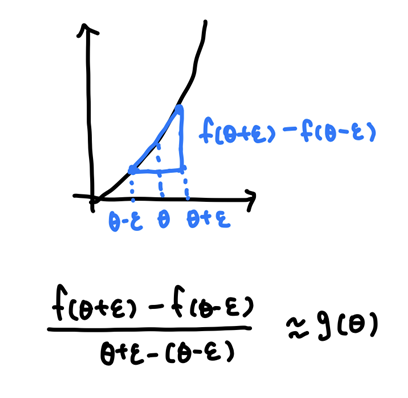
ex) ε=0.01

[(1.01)^3-(0.99)^3] / (2*0.01) = 3.0001

g(1) = 3 

-> 3과 3.0001은 약 0.001 차이 

 

즉, 두번째 방법이 훨씬 더 정확한 기울기 값에 근사하게 된다. 따라서 gradient checking을 할 때는 두번째 근사법을 사용하는 것이 더 정확하다. 

 

 

 

 Gradient Checking

 

 Gradient checking을 하기 위해서는 우선 매개변수들을 하나의 큰 벡터로 reshape 해주어야 한다. 

W[1], b[1], ..., W[L], b[L] -> big vector θ

dW[1], db[1], ..., dW[L], db[L] -> big vector dθ

이렇게 변화시킨 후 위에서 보았던 방식으로 gradient의 근사 값과 비교하여 gradient 계산이 맞게 되었는지 확인한다. 

 

 

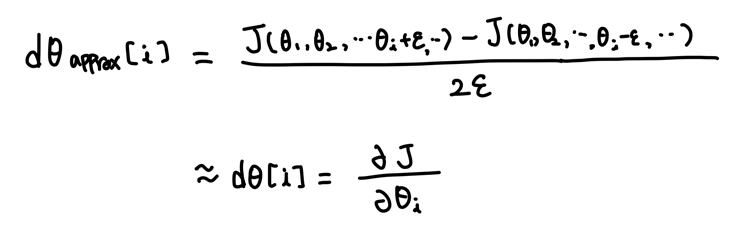
계산한 dθapprox 값과 dθ를 유클리드 거리로 비교하여

유클리드 거리 = ||dθapprox - dθ||2

 

거리 ≤ 10^(-7) -> great

거리  ≥ 10^(-3) -> worry

대략 이러한 기준으로 gradient checking을 한다. 

 

※ Gradient Checking Tip

- dθapprox를 계산하는데 시간이 오래 걸리기 때문에 training 단계에서는 하지 않는다.

- gradient checking을 했는데 "worry" 상태가 되었다면, 각 요소들을 살펴보기(?)

- dθ는 J의 정규화 항을 포함한다는 것을 기억하기

- dropout과 gradient checking은 함께 사용하지 않기

- 매개변수를 랜덤 초기화하고 훈련을 조금 시킨 후 gradient checking 하기