[Improving Deep Neural Networks: Hyperparameter Tuning, Regularization an Optimization] Hyperparameter Tuning, Batch Normalization and Programming Frameworks

Hyperparameter tuning

 

 Tuning Process

 

 하이퍼파라미터는 중요도에 따라서 튜닝을 진행해주어야 한다. 아래는 하이퍼파라미터 별 중요도 순으로 나열한 목록이다. 
① learning rate

② momentum(0.9), #hidden units, mini-batch size

③ #layers, learning rate decay

④ Adam: beta1(0.9), beta2(0.999), epsilon(10^-8) <- 거의 고정

 

 이제 이 하이퍼파라미터들을 선택하는 방법에 대해 알아보자. 하이퍼파라미터를 탐색하는 방법에는 그리드, 랜덤 탐색이 있다. 결론적으로 랜덤 탐색을 사용하는 것이 좋은데, 그 이유는 여러 하이퍼파라미터 중 어떤 것이 중요한지 모르기 때문이다. 참고로 하이퍼파라미터 수가 적을 때는 그리드 탐색이 가능한데 딥러닝을 사용할 때는 파라미터 수가 많기 때문에 사용이 어렵다. 

 무작위로 파라미터를 탐색하는 방법 중 조금 더 정밀한 방식으로 탐색하는 방법이 있다. 우선 전체에서 랜덤하게 탐색을 하고 범위를 점점 좁혀 더 작은 범위에서 랜덤 탐색을 진행하는 것이다. 

 

 

 

 Using an appropriate scale to pick hyperparameters

 

 학습률과 정규화 계수와 같은 하이퍼파라미터는 10^-6 ~ 10^-1과 같이 일반적으로 다양한 스케일을 가지는데, 이러한 값들을 선형 척도로 샘플링하면 대부분의 값이 매우 작거나 매우 큰 값에 집중이 되어 일부 중요한 범위를 놓칠 수 있다. 따라서 이러한 경우에는 로그척도를 사용하여 특정 범위에 치우치지 않고 전체 범위를 고르게 탐색해야한다.

 로그 스케일에서 샘플링하는 방법은 다음과 같다. 

 

 step 1) 값을 로그 스케일로 변환

  ex. 학습률이 10^-6, 10^-1까지의 범위에서 선택될 수 있다면 이 범위를 log(10^-6)=-6, log(10^-1)=-1 의 로그 스케일로 변환한다. 

 

 step 2) 로그 스케일에서 샘플링

  ex. [-6, -1] 범위에서 균등하게 값을 샘플링한다. 

 

 step 3) 지수 함수로 변환

  ex. 샘플링으로 -4.5를 얻었다면, 이를 다시 지수 함수로 변환하여 10^(-4.5)의 학습률을 사용한다.  

 

※ 지수 가중 평균에서의 하이퍼파라미터

 지수 가중 평균을 사용할 때 beta의 값은 0.9~0.999와 같이 표현된다. 이러한 값들은 1-beta를 사용하여 0.1~0.001과 같이 변환하여 로그 스케일 샘플링을 진행한다. 

 

 

 

 Hyperparameters tuining in practice: Pandas vs. Caviar

 

 실제 모델을 학습할 때 CPU, GPU와 같은 컴퓨터 자원의 양에 따라 모델을 학습하는 방법을 다르게 해주어야 한다. 학습 방법은 두가지로 구분할 수 있다. 

① Babysitting one model (컴퓨터 자원이 부족할 때) -> Pandas

 이 방법은 많은 컴퓨터 자원이 요구되지만 이를 충족하지 못할 경우에 사용하는 방법이다. "babysitting"의 의미는 아기를 돌보는 것처럼 한 모델의 성능을 실시간으로 모니터링하여, 성능이 기대에 미치지 못할 경우 하이퍼파라미터를 변경하는 등 즉시 조치를 취하는 방법을 말한다. 

 

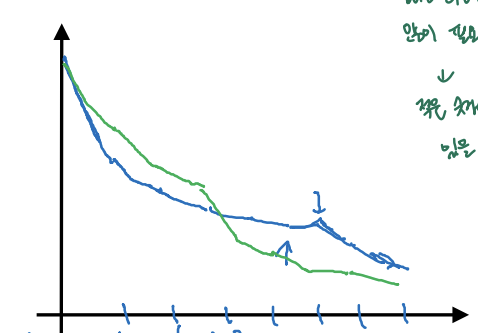
② Training many models in parallel (컴퓨터 자원이 충분할 때) -> Caviar

 이 방법은 컴퓨터 자원이 충분하여 여러 모델을 한 번에 훈련할 수 있을 때 사용하는 방법이다. 여러 모델을 동시에 훈련하면서 최고의 성능을 보이는 모델로 최종 모델을 선택하면 된다. 

 

 

※ pandas, caviar라고 비유한 이유는 판다는 새끼를 1마리 정도 낳아 애지중지 돌보는 동물이고, 물고기의 경우 한 번에 여러 알을 낳아 잘 성장한 새끼를 고르기 때문이다.

 

 

Batch Nomalization

 

 Normalizing activations in a network

  

 학습의 속도를 높이기 위해 입력에 normalization을 진행하는 과정을 배웠었다. 배치 정규화(Batch Normalization)란 이러한 과정처럼 입력층에만 정규화를 하는 것이 아니라 신경망 안 은닉층 값까지 정규화를 진행하는 것이다. 즉 하나의 층을 거치고 나서 얻은 정규화된 z[l] 값을 해당 배치에서 정규화하여 a[l]의 입력으로 사용한다. 정규화 식은 다음과 같다.

 

z(i)_norm = (z(i) - m) / root(variance + epsilon)

 

 여기서 z(i)_norm의 평균과 분산은 m(beta)과 root(variance + epsilon)(gamma)로 조정이 가능하다. 이 방법으로 정규화된 값의 평균을 0이 아닌 다른 값으로 갖게 하는 게 좋은데, 이는 활성화 함수(ex. sigmoid)의 비선형성을 살릴 수 있도록 하기 위함이다. 

 

z(i)_new =  gamma*z(i)_norm + beta

 

0에 치중된다면 시그모이드 함수가 선형 함수와 비슷하게 작동함

 

 위의 방식으로 배치 정규화를 진행한 값을 신경망에 사용하려면 우선 기존 방법과 똑같이 z[l]을 구한 후 z(i)[l]_norm을 계산하고 beta, gamma 값을 조정하여 z(i)[l]_new를 얻어 이 값을 a[l] 활성화 함수에 입력한다. 이처럼 배치 정규화를 이용하면 학습 속도가 빨라지지만 매개변수 수가 beta, gamma로 인해 증가한다. 여기서 beta는 모멘텀, RMSProp에서 사용되는 beta와 다르며 배치 정규화의 beta, gamma는 Adam, 모멘텀, RMSprop 방식으로 업데이트 가능하다. 

 참고로 배치 정규화를 사용하면 정규화 과정에 값의 평균을 빼기 때문에 b[l]의 역할이 사라져 매개변수 b는 사용하지 않는다. 따라서 여기서는 b[l]의 역할은 z(i)[l]_new를 만들 때 사용하는 beta 값이 대신하게 된다.(결과적으로 편향 변수를 결정하기 때문) 

 

 

 

Multi-class classification

 

 Why does Batch Norm Work?

 

 딥러닝 모델을 학습하다보면 각 층의 입력 분포가 변화하는 "내부 공변량 변화"가 발생한다. 각 층의 파라미터가 업데이트되면 다음 층의 입력 분포가 계속해서 변하게 되는데, 이러한 변화는 학습을 불안정하게 만들고 학습 속도를 저하시킨다. 또 입력 데이터가 달라졌을 때도 배치 정규화로 값의 평균과 분산을 유지하여 모델의 학습을 안정화시킨다. 

 다음으로 배치 정규화는 regularization 역할을 하며 과적합을 방지하기도 한다. 우선 배치 정규화는 노이즈 주입 효과가 있다. 배치 정규화는 미니 배치마다 평균, 분산을 구해 계산하므로 미니 배치마다 계산된 값이 다르다. 이로 인해 모델은 일정한 노이즈가 주입된 것처럼 동작하게 되고, 이는 드롭아웃과 같은 유사한 정규화 효과를 가져온다. 그리고 미니 배치마다 값이 달라지는 것으로 모델이 특정 패턴에 과적합되는 것을 방지한다. 하지만 배치 정규화는 regularization 목적이 아니므로 사용할 때는 학습 속도 향상을 목적으로 사용해야한다. 

 

 

 

 Batch Norm at Test time

 

 학습 중에서는 배치 정규화가 각 층마다 각 미니 배치의 평균과 분산을 사용하여 활성화 값을 정규화한다. 하지만 테스트 중에는 각 미니 배치의 평균과 분산을 사용할 수 없다. 따라서 테스트에서는 학습 과정에서 계산된 평균과 분산의 지수 가중 평균을 사용하여 정규화를 수행한다. 그리고 γ와 β는 학습된 값을 사용한다. 

 

 

 

 Softmax regression 

 

 다중 클래스를 분류할 때 softmax 함수를 사용해보겠다. 아래는 4가지 클래스로 입력 이미지를 분류하는 신경망이다. 

 

 

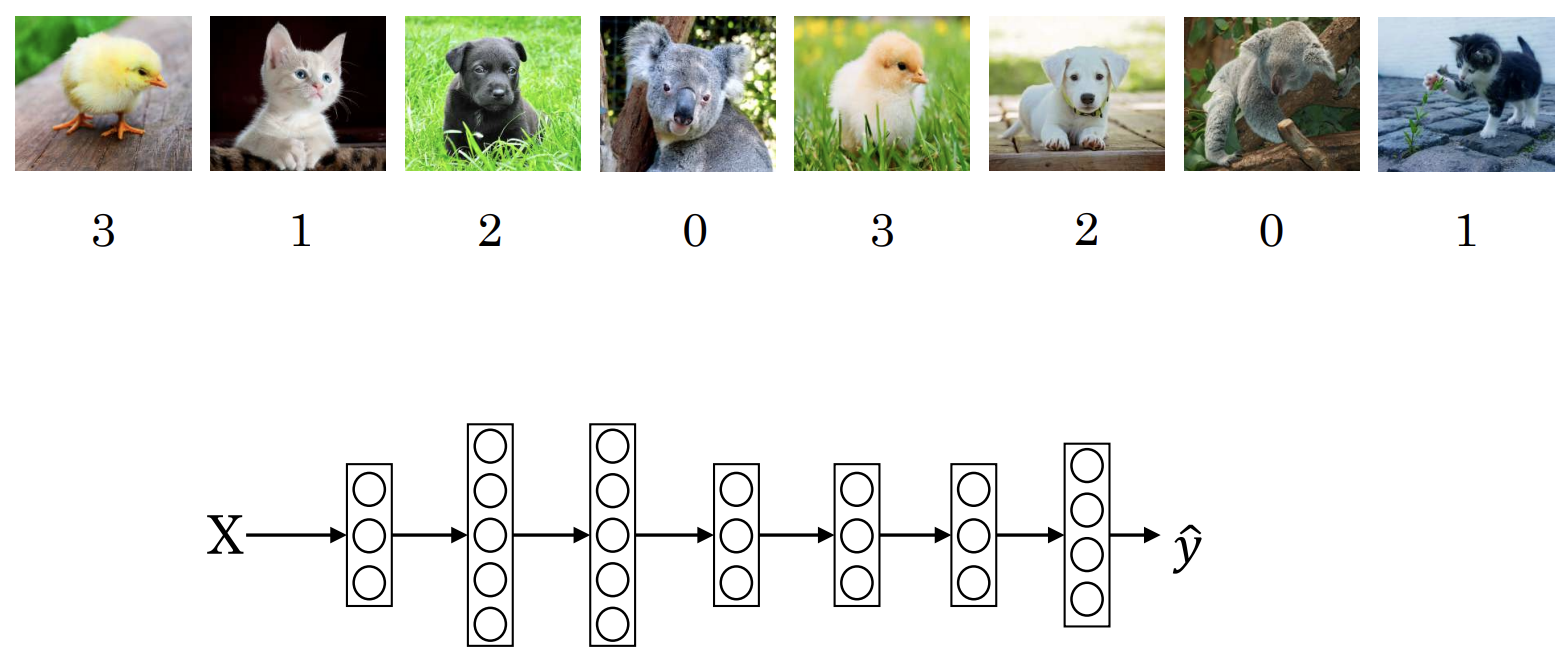
 마지막 레이어의 4개 유닛에서는 각 입력에 대해 softmax 함수를 적용해 입력 이미지가 각 클래스에 해당할 확률을 계산한다. 4개의 확률을 합치면 100% 확률이 계산된다. 

 만약 이러한 softmax regression을 사용할 때 신경망에 은닉층이 없다면 두 클래스 사이의 경계는 선형이 된다. 반대로 신경망에 은닉층이 있다면 두 클래스 사이 경계는 복잡한 비선형 경계가 된다. 

은닉층이 없을 때의 경계

 

※ 참고로 softmax의 반대는 hardmax인데, hardmax는 가장 큰 결과 값을 가지는 곳에 1을 갖고 나머지에 0을 갖는 벡터로 대응된다.