juuuding
[CS231n] Lecture 4. Backpropagation and Neural Network 본문
최적화를 하기 위해 w가 변화함에 따라 Loss 값이 어떻게 바뀌는 지 알아야 한다. gradient descent로 parameter 값이 변할 때 loss가 얼마나 변하는지 알아낼 수 있는데, 여기서 우리는 "Backpropagation" 과정을 이용하여 빠르고 쉽게 gradient descent를 계산해낼 수 있다.
Backpropagation
[Computational graphs]
Backpropagation 과정을 잘 표현하기 위해 "Computational graph"라는 계산 과정을 그래프로 나타낸 그림을 이용할 것이다. 각 노드는 계산 과정을 나타내고 노드들은 엣지로 이어서 표현한다.

[Backpropagation]
다음은 역전파(Backpropagation)의 간단한 예시이다. 우선 식을 computational graph로 표현하였는데 아래와 같이 왼쪽에서 오른쪽으로 계산하는 것을 순전파(forward propagation)이라고 한다.


역전파를 이용하여 우리가 얻고자 하는 값은 x,y,z가 변함에 따라 달라지는 f의 값이다. 이를 구하기 위해 미리 구해 놓을 수 있는 값들을 계산해둔다.

이제 위 값들을 가지고 반복되는 chain rule을 이용하여 역전파를 진행할 것이다. 역전파이기 때문에 순전파와 반대로 오른쪽 끝부터 시작한다. 먼저 f에 대한 f의 도함수 값을 구한다(1).

다음으로 z에 대한 f의 도함수 값을 구한다. 이 값은 위에서 미리 구해 놓았기 때문에 바로 q라는 것을 알 수 있다. q는 x+y이므로 -2+5=3이다.

이제 q에 따른 f의 도함수 값을 구한다. 이 값도 위에서 z로 계산해 놓았기 때문에 -12=3*z 로 z=-4 라는 것을 바로 알 수 있다.
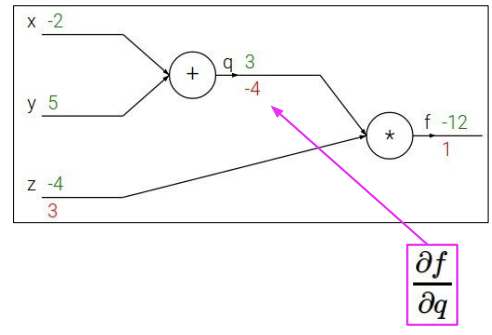
다음으로 우리가 원하는 값 중 하나인 y에 대한 f의 도함수 값을 구한다. 이 값은 chain rule를 이용하여 표현할 수 있는데, y에 따른 q의 변화 값(a)과q에 따른 f의 변화 값(b)으로 chain rule을 사용한다. a는 위에서 1로 미리 구해놓았고, b는 바로 위에서 -4로 구해놓았으니 1*-4를 하여 y에 대한 f의 도함수 값 역시 -4인 것을 알 수 있다.
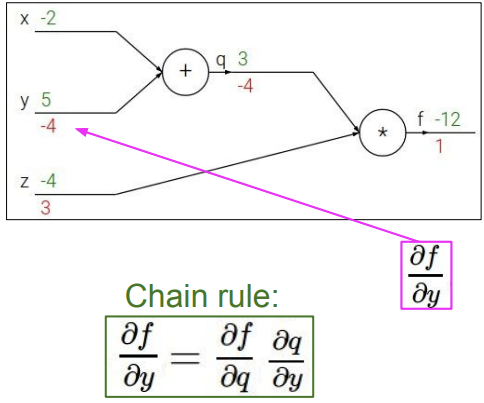
마지막으로 x에 대한 f의 도함수 값을 구한다. 여기서도 chain rule을 이용하여 x에 대한 q의 도함수 값(a)과 q에 대한 f의 도함수 값(b)을 사용하여 값을 구할 수 있다. 여기서 a는 1 b는 -4로 1*-4를 하여 x에 대한 f의 도함수 값이 -4라고 할 수 있다.
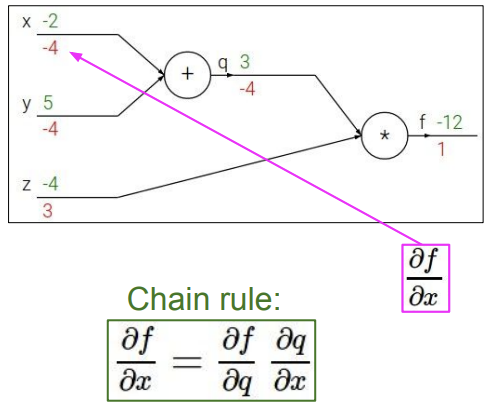
이처럼 역전파에서는 chain rule을 이용하여 우리가 원하는 도함수 값들을 구해낸다. chain rule을 사용할 때는 local gradient와 앞에서 구해놓은 upstream gradient을 쓴다.

다음은 위의 계산보다 조금 더 복잡한 역전파 예시이다. 아래는 chain rule을 이용하여 역전파의 과정들을 진행한 결과이다. 위의 과정과 똑같이 local gradient와 upstream gradient를 이용하여 원하는 결과 값을 얻을 수 있다.
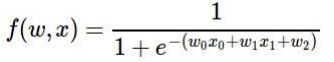
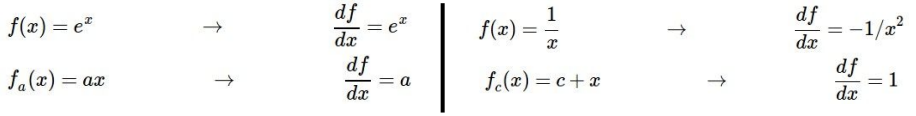
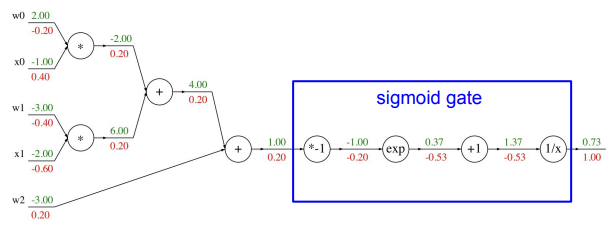
파란 박스는 sigmoid function 계산 과정을 computational graph로 표현해놓은 것인데, 이처럼 local gradient를 작성할 수 있어 그룹화가 가능한 연산은 좀 더 복잡한 노드 하나로 묶어도 된다. sigmoid function의 gradient는 다음 식으로 표현할 수 있다.

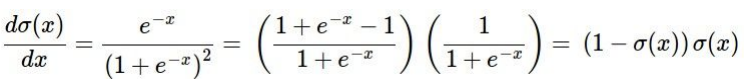
이 식을 가지고 sigmoid function의 계산 과정을 하나로 축약시킬 수 있다.
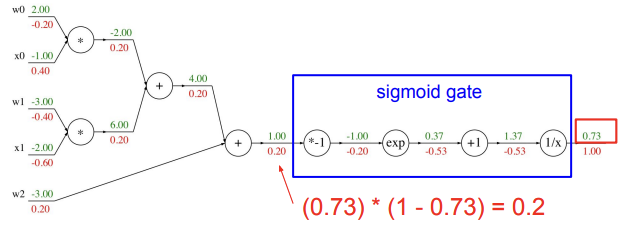
[Patterns in backward flow]
역전파를 하며 각 계산 노드의 종류마다 패턴들이 있다. 따라서 add, max, mul gate의 각각 특성에 대해 알아볼 것이다.
① add gate
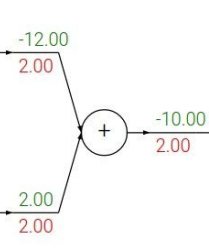
더하기 노드로 합쳐지는 gate는 "gradient distributor"라는 특성이 있다. add gate에서는 local gradient가 각각 1이기 때문에 upstream gradient가 그대로 양쪽에 주어진다.
② max gate
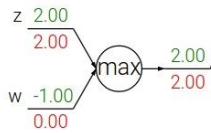
max gate는 두 input 값 중 큰 수를 선택하는 것이다. 여기서는 둘 중 한 쪽만 upstream gradient를 이어 받고 나머지 하나는 0으로 설정된다. upstream을 이어 받는 쪽은 input 값이 더 큰 쪽이다. 이처럼 max gate에서는 한 쪽으로 gradient를 넘겨주기 때문에 "gradient router"라고 할 수 있다.
③ mul gate
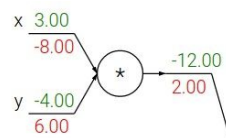
mul gate는 두 input 값을 곱하는 gate이다. 이 gate에서의 local gradient는 각각 자신이 아닌 상대의 input 값이 되므로, upstream gradient를 곱한 최종 gradient는 상대 input 값 * upstream gradient가 된다. mul gate에서는 서로 다른 branch로 값을 scale하는 것을 알 수 있다. 따라서 mul gate는 "gradient switcher"라는 특성이 있다.
[Gradient add at branches]
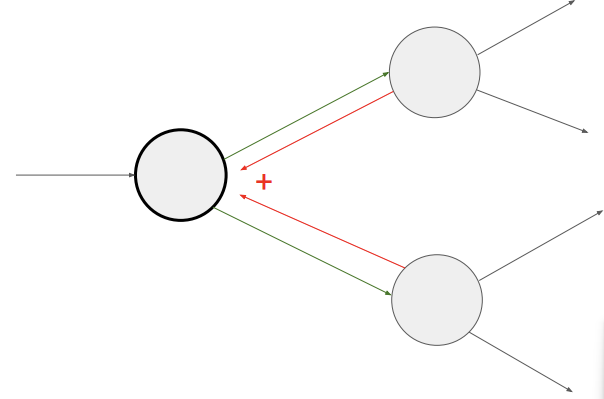
그림과 같이 역전파 관점에서 두 노드가 하나로 합쳐질 때 즉, upstream gradient가 한 곳으로 모일 때는 단순히 두 gradient를 더하면 된다.
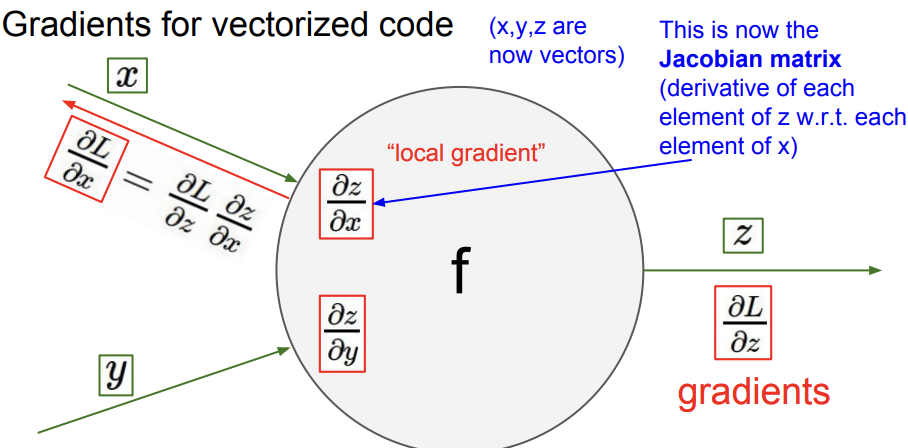
[Gradient for vectorized code]
이제 gradient가 Jacobian matrix가 된 경우에 대해 알아볼 것이다. x,y,z는 이제 벡터 값을 가진다.
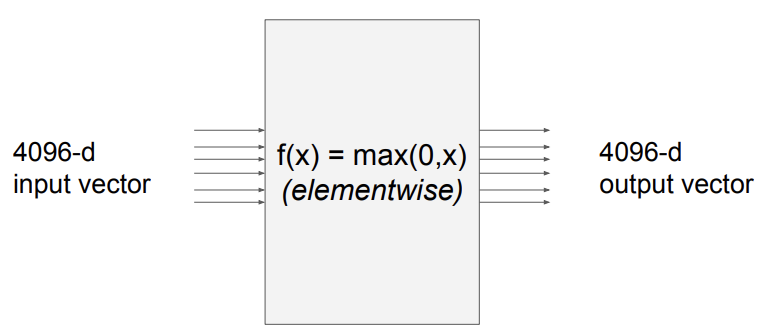
input과 output이 4096-d의 벡터이고 중간에 max 함수 f를 거친다.
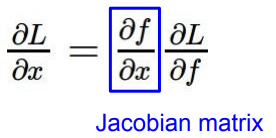
Q) Jacobian matrix의 크기는?
- 모든 행이 output의 각 차원에 대하여 input의 각 차원과 partial derivative한 행렬이기 때문에 4096*4096의 크기를 가진 행렬이 된다. 참고로 실제에서는 minibatch를 이용하여 4096의 크기를 가진 jacobian을 모두 계산할 필요는 없다.
Q) 어떤 형태로 나타나는가?
- input은 output에 각각 대응되는 요소에만 영향을 미치므로 diagonal matrix의 형태로 나타난다.
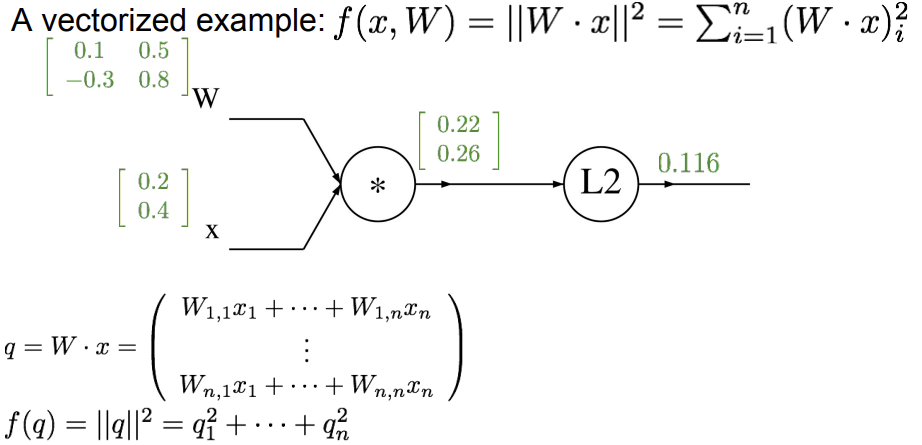
위는 행렬 계산을 하여 결과 값을 얻어낸 예시다. 이제 이것을 가지고 역전파를 수행해보자.
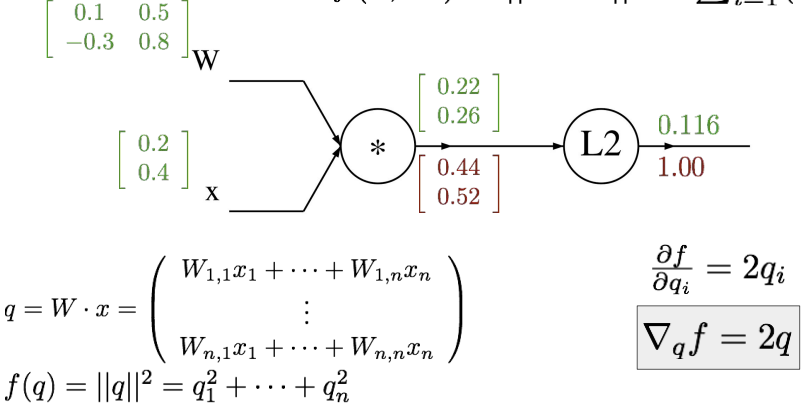
위에서도 알 수 있듯이 gradient vector의 크기는 original vector와 같고, gradient의 각 요소는 output에 얼마나 영향을 미치는 지에 대한 정보이다.
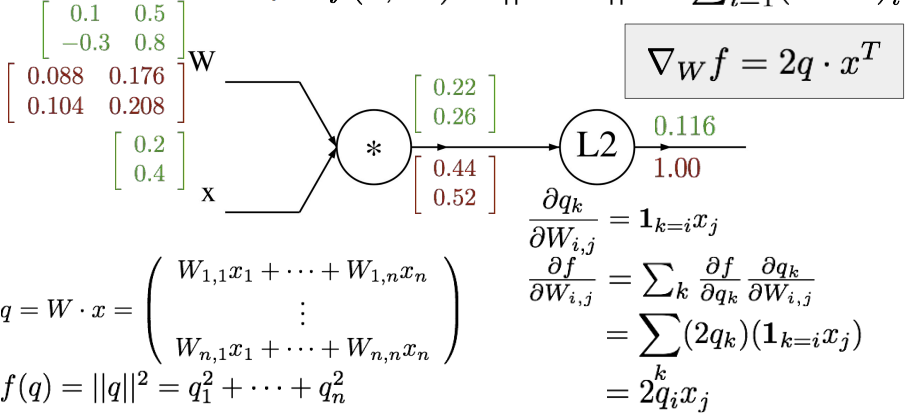
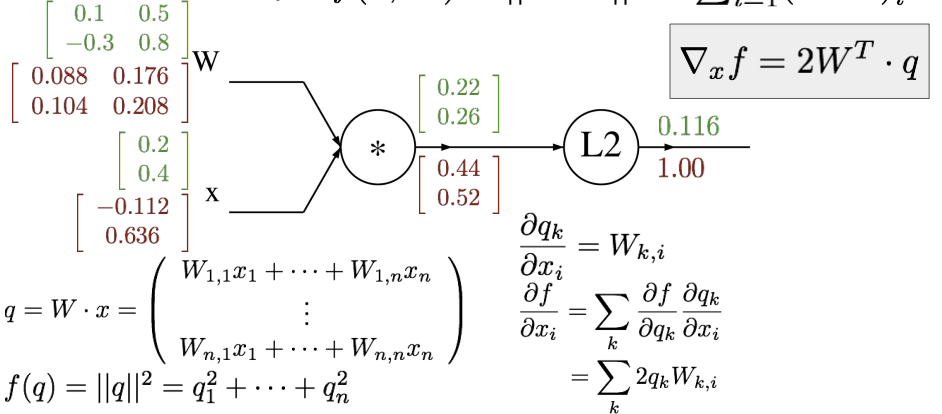
위와 같은 과정으로 w에 대한 f의 도함수 값도 계산한다. 마찬가지로 original matrix와 gradient matrix의 크기가 같은 것을 확인할 수 있다. 마지막으로 x에 대한 f의 도함수 값을 계산해주면 다음과 같은 결과가 나온다.
Neural Networks
이 전에는 단순한 하나의 linear score function을 사용했다고 하면, 지금은 Neural Network를 이용하여 여러 식을 겹쳐 계산이 가능해졌다.

그렇기 때문에 linear classifier에서 보았던 것처럼 한 템플릿으로 물체를 구별해야했던 때에는 많은 오류들이 발생할 수 있었지만, neural network를 사용하면서 이러한 오류의 발생을 줄일 수 있게 되었다. 예를 들어 아래의 템플릿 하나로 물체를 구별해야 할 때는 만약 car이 템플릿처럼 빨간색이 아니면 car이라고 분류하지 못하는 경우가 있었다. 하지만 neural network를 사용하면서 빨간차, 노란차, 파란차 등을 합칠 수 있기 때문에 여러 다른 색의 차도 정확히 분류될 수 있게 되었다.

이러한 neural network는 biological neural network의 영향을 받아 만들어진 것인데, 다음으로 어떤 영향을 받았는지 알아볼 것이다.
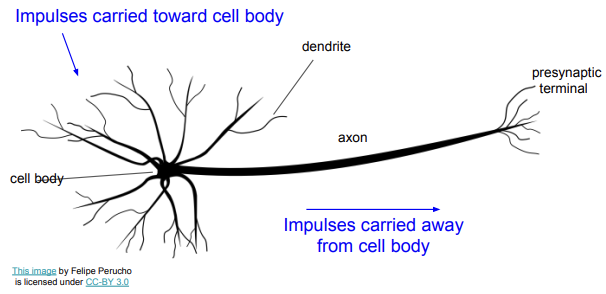
이는 생물학적 신경망 그림이다. cell body에서는 신호를 가지고 그 신호들을 모두 해석해내는 역할을 수행한다. dendrite에서는 뉴런으로 들어오는 자극을 받는 역할을 하고, axon은 이 자극을 옮기는 역할을 한다. 우리가 사용한 신경망도 이것과 유사한 방식을 가진다.
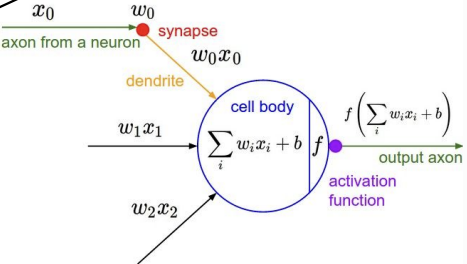
axon에 의해 전달된 자극을 dendrite가 받고 cell body에서 이 자극을 가지고 계산을 수행한다. 그리고 이 결과를 output axon에 넘겨 주면서 다른 cell body로 신호를 전달한다. 참고로 synapse는 여러 뉴런을 연결하는 역할을 한다.
이처럼 원리는 생물학적 신경망으로부터 영향을 받았지만 생물학적 뉴런이 아주 훨씬 더 복잡하다.
[Activation functions]
다음은 활성화 함수의 종류 6가지다.
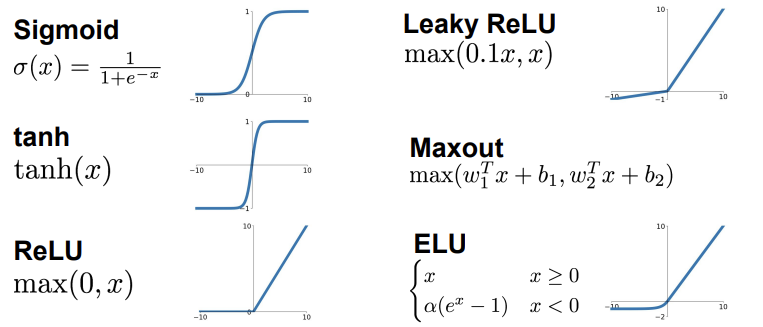
[Neural Networks: Architectures]
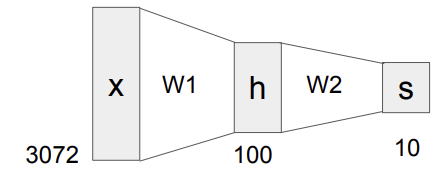
다음은 neural network architecture의 서로 다른 종류이다. (layer의 개수가 다름)
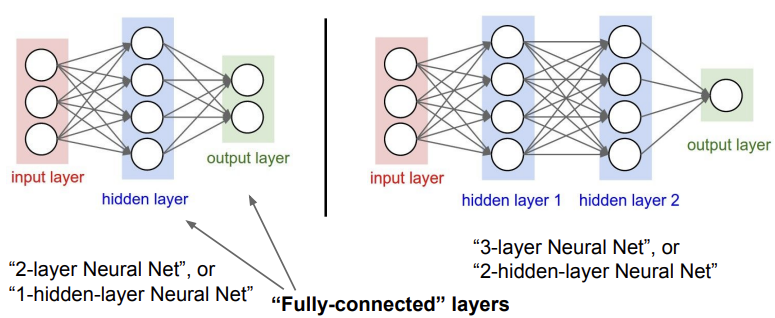
오른쪽 그림과 같이 3-layer Neural Net은 아래와 같은 코드로 표현할 수 있다.

'인공지능 > cs231n' 카테고리의 다른 글
| [CS231n] Lecture 6. Training Neural Networks, Part 1 (0) | 2024.01.25 |
|---|---|
| [CS231n] Lecture 5. Convolutional Neural Networks (2) | 2024.01.03 |
| [CS231n] Lecture 3. Loss Functions and Optimization (2) (1) | 2023.12.08 |
| [CS231n] Lecture 3. Loss Functions and Optimization (1) (0) | 2023.12.07 |
| [CS231n] Lecture 2. Image Classification (1) | 2023.11.28 |




