[Advanced Learning Algorithms] Neural Networks - Vectorization

 How neural networks are implemented efficiently

 

 neural network를 for loop와 vectorization을 사용하여 수행할 수 있다. 아래의 코드에서 보다시피 vectorization이 코드가 더 간결하고, 속도가 더 빠르기 때문에 vectorization을 사용하는 것이 더 좋다.

 

[For loops]

x = np.array([200,17])
W = np.array([1,-3,5],
    	     [-2,4,-6]])
b = np.array([-1,1,2])

def dense(a_in,W,b):
	units = W.shape[1]
    a_out = np.zeros(units)
    for j in range(units):
    	w = W[:,j]
        z = np.dot(w,x) + b[j]
        a[j] = g(z)
    return a

 

 

[Vectorization]

X = np.array([[200,17]])
W = np.array([1,-3,5],
    	     [-2,4,-6]])
B = np.array([[-1,1,2]])

def dense(A_in,W,B):
	Z = np.matmul(A_in,W)+B
    A_out = g(Z)
    return A_out

 

 참고로 Vectorization에서는 모든 데이터를 2차원 배열로 저장하여 계산한다. 그렇기 때문에 괄호를 2번 사용하여 배열을 표현해야 한다. 결과 값도 2차원으로 표현된다. 

 

 

 

 Matrix multiplication

 

[Dot products]

 행렬의 dot product는 아래의 예시처럼 수행한다. 

 

 

z = a·w

z = (1x3) + (2x4)

 

 

 이러한 dot product는 a를 transpose를 하여 multiplication 형태로 바꿀 수 있다.

 

 

 

 transpose는 다음과 같이 행과 열을 바꾸는 과정이다.

 

 

 

 

 

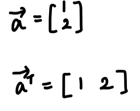
[Vector matrix multiplication]

 

 

[Matrix matrix multiplication]

 

 

 

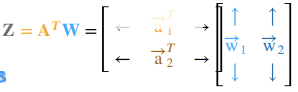
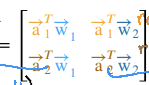
 Matrix multiplication rules

 

[Matrix multiplication rules]

 

 이처럼 행렬끼리 곱셈을 할 때는 앞 행렬의 행, 뒷 행렬의 열 위치에 맞추어 결과 값을 계산한다. 

 

 

 

 Matrix multiplication code

 

[Matrix multiplication in Numpy]

 

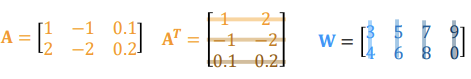
 위의 matrix multiplication 과정을 numpy로 작성해보겠다.

 

import numpy as np

A = np.array([[1,-1,0.1],
              [2,-2,0.2]])
AT = A.T
W = np.array([[3,5,7,9],
             [4,6,8,0]])

Z = np.matmul(AT,W)
print(Z)

 

 

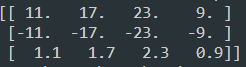
 참고로 T는 행렬을 transpose 해주는 함수이고, matmul은 행렬의 곱셈을 수행해주는 함수이다. 

 

 

[Dense layer vectorized]

 

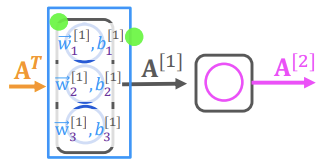
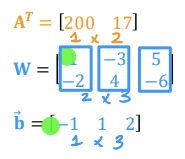
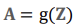
 위의 식을 가지고 dense 함수를 코드로 표현하면 다음과 같다. 

 

import numpy as np

AT = np.array([[200,17]])
W = np.array([[1,-3,5],
              [-2,4,-6]])
b = np.array([[-1,1,2]])

def dense(AT,W,b,g):
    z=np.matmul(AT,W) + b
    a_out = g(z)
    return a_out