juuuding
[Open SW Project] Lec02_Image display and geometric transform 본문
[Open SW Project] Lec02_Image display and geometric transform
jiuuu 2025. 1. 23. 17:41💡Image quality
Image quaity는 이미지가 sharp 하고 detail 한 정도를 의미한다. sharp한 정도는 spatial resolution(해상도)로 판별하고, detail한 정도는 intensity quantization으로 판별한다. 이해하기 쉽게 생각하자면 한 이미지를 얼마나 많은 픽셀로 촘촘히 나누는지에 따라 sharp한 정도가 정해지고, 이 픽셀에 얼마나 다양한 intensity 값이 들어갈 수 있는지로 정해진다.
spatial resolution 값을 낮추게 되면 같은 이미지를 적은 픽셀로 표현하기 때문에 사진이 흐릿하게 보인다. 그와 달리 intenstity quantization을 낮추면 흐릿해지기보다는 좀 더 색감이 자연스럽지 못하고 디테일이 떨어져 보이게 된다.



[Intensity Quantization]
quantization 조절하는 방법을 알아보자. 만약 원본 이미지의 intensity 범위가 0~255라고 하자. 즉 intensity를 표현하는데 8bit를 사용하는 것이다. 이를 줄여서 3bit로 intensity를 표현한다고 하자. 그러면 intensity의 범위가 0~7이다. 이렇게 되면 256개로 표현하던 것을 8개로 표현해야 하는데, 그러면 원래는 다른 intensity 값을 가졌던 픽셀이 같은 값을 가질 수도 있다. 예를 들어, 원래 a 픽셀의 값이 225였고 b 픽셀 값이 250이였는데 이 둘을 3비트 표현으로 줄이면 두 값 모두 7로 같은 값을 가지게 된다. 그럼 원래 다른 색이였던 픽셀이 같은 색이 돼버리는 것이다. 이렇게 된다면 당연히 이미지의 디테일이 떨어진다.



[Spatial Resolution]
Spatial resolution을 크게 한다는 것을 같은 이미지를 더 많은 픽셀을 이용해서 표현한다(display)는 것이다. 만약 아래의 픽셀을 가진 이미지를 단순히 반으로 줄인다면, 4개의 픽셀마다 1개의 픽셀을 선택해서 표현한다. 그러고나서 이 줄어든 이미지를 다시 원본 크기로 돌려놓으려면 이미지 크기를 2배 해주어야 하는데, 이 때 나머지 3개의 픽셀에 하나의 픽셀 값을 똑같이 채워 주어야 한다. 그러면 원래 각각 다른 값을 가졌던 픽셀들이 같은 값으로 채워지게 된다.
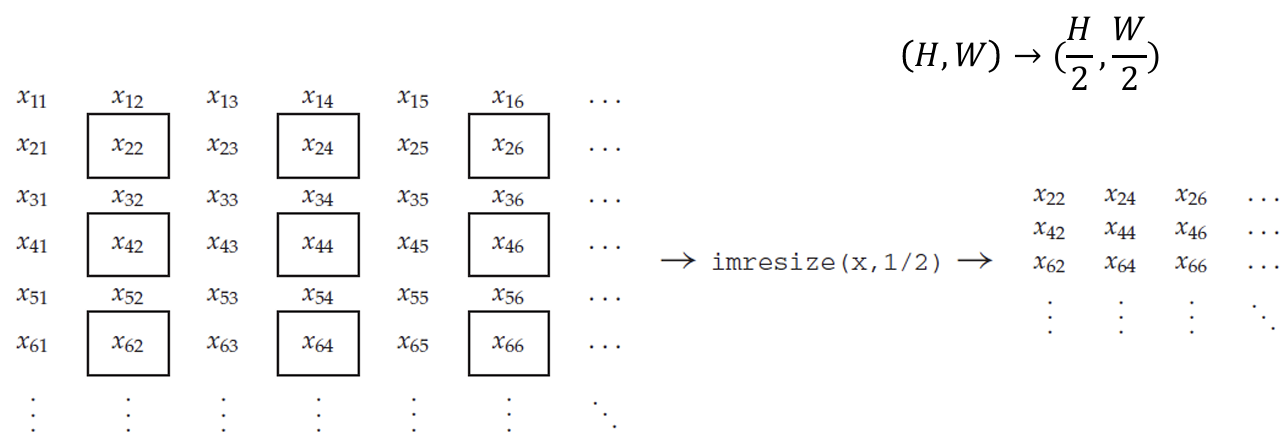

여기서 imresize의 param 값은 src 값, n배 resize 값이다.
이걸 resolution 측면에서 해석해보자. 원본 이미지의 크기를 줄였다가 다시 크기를 되돌려 놓는데, 줄어들었던 픽셀들에 해당하는 intensity 값들이 한 pixel의 intensity 값과 같은 값으로 설정된다. 이렇게 되면 원래 4개의 픽셀로 나누어졌던 것들이 4배로 커진 하나의 픽셀로 보이게 된다. 그러면 한 이미지를 구성하던 픽셀들의 개수가 줄어든 것과 같은 효과가 발생한다.
이 개념의 의미와 사진에 적용되는 효과는 이해가 가는데, 픽셀 개념을 잘 모르겠어서 정확하게 설명하지 못하겠다. 글 가장 아래에 헷갈리는 부분들을 작성해두었다.



quantization을 조절했을 때는 blurry 효과가 발생했지만, 이와 다르게 resolution에서는 네모 상자가 뚜렷하게 보이는 box effect가 발생한다. 이 두 방식이 이러한 차이를 보이는 원인은 "upsampling" 방식의 차이 때문이다. 결론부터 말하자면 quantization에서는 bilinear upsampling 방식을 사용하고, resolution에서는 nearest neighbor upsampling을 사용한다.
💡 Interpolation
Interpolation(보간)이란 주변 픽셀들의 값으로 한 픽셀의 값을 estimate 하는 것이다. estimate 하는 방법에 따라 interpolation 종류가 NN(Nearest Neighbor) interpolation, Bilinear interpolation, Bicubic interpolation, Lanczos interpolation 등으로 나뉜다.
* 참고로 Linear interpolation과 Bilinear interpolation은 operation 방식은 같지만 1차원이냐 2차원이냐로 차이가 나는 것이고, 마찬가지로 Cubic interpolation(1차원), Bicubic interpolation(2차원)도 operation 방식은 같고 차원만 차이가 난다.
- Nearest-Neighbor interpolation
단순히 이웃의 intensity 값을 copy and paste 하는 방식이다.

- Linear interpolation
이웃의 intensity 값을 선형 방정식(f(m) = am+b)을 사용해서 반영하는 방식이다.

아래와 같이 proportional linear equation을 사용해서 표현할 수도 있다.

간단하게 생각하면 x1에 가까울수록 람다 값이 작고 1-람다 값이 커지는데, 가까우니 더 큰 영향을 받아야 하니 1-람다 값을 f(x1)에 곱하는 것이다. 이걸 linear interpolation이라고 하는데, 다음으로 이를 2D에서 다루는 bilinear interpolation에 대해 알아보자.
- Bilinear interpolation(2D)
2차원에서는 앞서 본 linear 과정을 3번 반복해주면 된다. vertical 2번, horizontal 1번 혹은 horizontal 2번, vertical 1번과 같은 방식으로 진행하면 Bilinear interpolation이다. 참고로 어떻게 하든 모두 결과가 같다.

[General Form of Interpolation]
위에서 본 interpolation을 general form으로 표현하면 다음과 같이 표현할 수 있다.
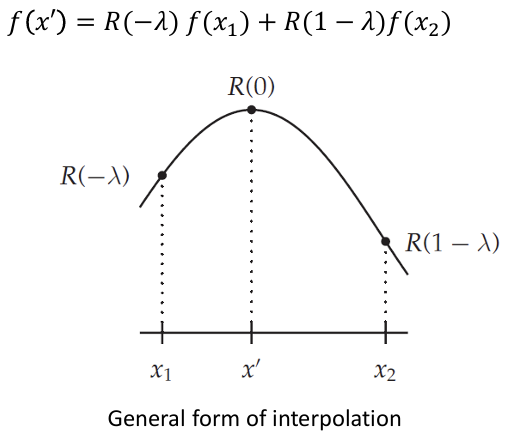
위 그래프 R은 interpolation에 반영 비율을 나타내는 함수다. 따라서 f(x1)과 f(x2)를 interpolation해서 f(x')를 얻을 때, 각각 얼마씩 값을 반영하면 될지를 얻어 계산할 수 있다. 이 general form을 가지고 NN과 linear interpolation을 표현해보겠다.
(1) NN interpolation
이에 해당하는 R 함수를 그리면 다음과 같다. NN은 가장 가까운 이웃의 값을 copy&paste 하는 것이므로 아래와 같이 직선으로 그려진다.

따라서 윗 그림에서 f(x')의 값을 estimate 하면, x'가 x1과 더 가깝기에 f(x1)의 값을 그대로 가져온다.
(2) Linear interpolation
이번에는 Linear interpolation을 general form으로 표현하면 다음과 같다. linear의 R 함수를 표현하면 1+u, 1-u로 작성되며, 이 R을 가지고 f(x')의 값을 interpolation으로 estimate해서 식을 정리하면 아까 보았던 linear interpolation의 식과 똑같이 정리된다.

(3) Cubic interpolation
주변 4개의 픽셀을 반영하여 interpolation 하는 cubic interpolation의 경우에는 다음과 같은 식으로 표현된다.


(4) Bicubic interpolation
Bicubic은 2차원에서 4개의 주변 픽셀을 반영하여 interpolation 하는 방법이다. 2차원이기 때문에 실질적으로는 총 16개 픽셀의 영향을 받는다. 우선 horizontal 방향으로 각 점에 대해 총 4번의 cubic interpolation을 하고, 그렇게 얻은 4개의 점을 가지고 다시 vertical 방향으로 cubic interpolation을 한다. 따라서 최종 5번의 cubic interpolation을 하면 결과 값을 얻을 수 있다. bilinear 때와 마찬가지로 horizontal 과 vertical를 반대로 적용해도 똑같다.(vertical 4번 horizontal 1번).
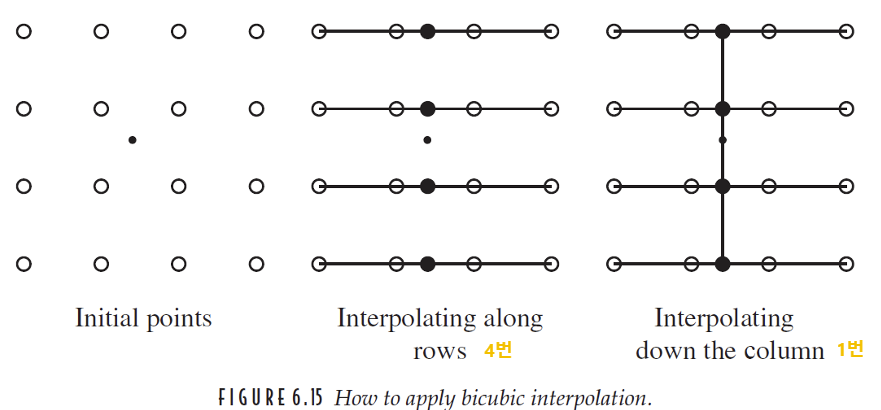
앞서 살펴보았던 interpolation을 사진에 각각 적용한 결과다. 여기선 bilinear과 bicubic의 차이가 확연하게 느껴지지 않지만, 보통 bicubic interpolation이 가장 좋은 결과를 보인다.

💡Geometric transformation
[more general transformation]
- translation, rotation, scale, skew 등.
[2D parametric transformation]
다음은 2차원 이미지에서의 transformation 종류들이다. 각 transformation 마다 다양한 개수의 param이 필요하다. 참고로 3D parametric transformation도 있는데, 2D에서 쉽게 확장할 수 있기에 2D에서의 원리를 알아보겠다.
- Translation
- Rigid(Euclidean) transformation
- Similiarity transformation
- Affine transformation
- Projective transformation

위 transformation 들의 결론부터 정리하자면 아래와 같다.
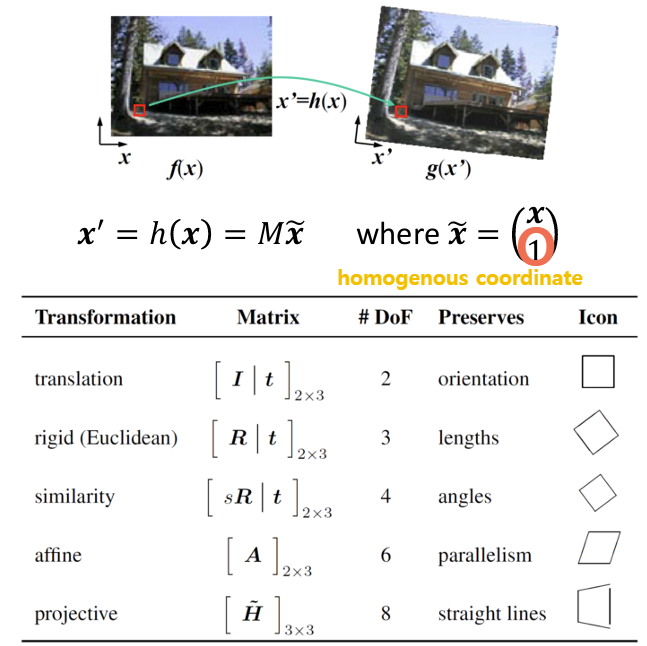
* #DoF 이란 Degree of Freedom으로 변환 행렬에서 독립적인 param의 수를 나타낸다.
- translation
translation은 단순히 이미지를 이동하는 것이다. 따라서 그냥 x, y좌표를 특정 값만큼 이동해주면 된다. 이 transformation 과정을 행렬로 나타내면 다음과 같다.

이 변환에서는 각 x,y 좌표를 얼만큼 이동할 것인지에 대한 정보 tx, ty만 있으면 되기에 DoF는 2다. translation 변환을 하면 이미지의 orientation, length, angle, parallelism, straight line 등은 유지가 된다.
- rigid (Euclidean)
rigid transformation은 물체의 크기나 모양이 변하지 않는 변환이다. 따라서 여기에는 rotation, translation이 속한다. 이 변환을 행렬로 표현하려면 회전을 하고 이동을 시킬 수 있는 행렬로 작성해야한다.

삼각 함수로 표현된 부분은 회전을 시키는 부분이며, 나머지 t 부분은 이동을 시키는 부분이다. 여기서는 theta, tx, ty 값이 필요하므로 DoF는 3이다. 참고로 DoF는 "독립적인" param이라고 했기에, cos과 sin가 아니라 theta를 고려해야한다. rotation을 하면 orientation은 보존되지 않고, 나머지 length, angle, parallelism, straight line 등이 보존된다.
- similarity
기하학에서 닮음은 유클리드 공간에서 모든 각을 보존하고, 모든 거리를 일정한 비율로 확대 또는 축소하는 변환이다. 따라서 rigid translation에서 객체를 회전하고 크기를 변환하는 것까지 할 수 있다. 일정한 비율로 크기를 변환해야하기에 크기와 관련한 매개변수는 딱 하나만 존재해야한다. 그렇기 때문에 이 변환은 DoF는 s(scaling), theta, tx, ty 로 4다. 닮음에서는 길이가 보존되지 않을 수 있으므로, 나머지 angle, parallelism, straight line 등이 보존된다.
- affine
affine transformation은 간단히 말하자면 transformation 후 linearity와 parallelism을 유지하는 변환이다. 따라서 translation, rotation, scale, skew 등을 포함한다. 컴퓨터 그래픽스 시간에 배운 내용을 잠시 떠올리자면 객체를 카메라로 찍어 screen에 project할 때, parallel하게 project가 되지 않으면 원근 정보(view point와의 거리)에 따라 선이 왜곡되어 표시된다. 그러면 원래 평행했던 line이 평행하지 않게 변형이 되어 parallelism이라는 특성을 잃게 된다. 어쨌든 이러한 왜곡이 발생하지 않도록 하는 transformation이 affine transformation이라고 말할 수 있다.
affine 변환 행렬은 원하는 변환에 맞는 2x3 행렬로 구성되어 있는데, 행렬의 각 요소는 서로 독립적인 관계로 존재하기에 총 6개의 매개변수가 필요하다.
- projective
projective transformation은 흔히 스마트 폰에서 문서를 스캔할 때 사용되는 변환이다. 위에서 언급한 것처럼 카메라로 객체를 찍어 screen에 project할 때 발생하는 변환인데, 여기서는 3차원 공간 정보 즉 깊이 정보를 포함해서 2차원 공간인 screen에 display 해야하므로 parallelism 특성을 잃게 된다. 이때도 마찬가지로 각 요소가 서로 독립적인 관계로 존재하는 매개변수가 필요한데, 3차원 결과가 나와야 하므로 3x3 행렬로 표현되어야 한다. 여기서 3차원 결과라 해서 헷갈릴 수 있는데, 2차원 공간으로 project 할 때 원근 정보까지 모두 계산 후, x,y 값을 w값(원근)로 나누고 x,y 값만 가져와 사용하는 원리다. 즉, transformation 계산 후 homogeneous coord로 변환한 뒤 x,y 좌표만 잘라서 쓰는 것이다.
다시 본론으로 와서 projective transformation은 3x3 행렬로 표현되어야 하는데, 그러려면 원래 총 9개의 매개 변수가 필요해진다. 하지만 여기서 1을 뺀 8이 이 변환의 DoF이다. 그 이유는 3행 3열의 값은 1로 고정되어야 하기 때문이다. homogenous coord에서 w 값을 원근에 따라 배율 변화 해주는 것은 괜찮지만, 덧셈/뺄셈의 연산이 들어가면 원래 좌표가 기존 비율과 맞지 않게 왜곡이 될 수 있다. 따라서 3행 3열의 값은 고정되어야 하기 때문에 DoF는 8이다.
[Geometric Transformation]
image warping이란 기존 이미지를 새로운 위치로 매핑하면서 이미지의 모양을 변형시키는 것을 말한다. 그 중 forward warping은 transformation을 하고 나서 바뀐 위치에 똑같은 픽셀 값을 copy&paste 해주는 방식이다. 그런데 이런 방식으로 warping을 하다 보면, 모든 픽셀이 원래의 비율에 맞지 않게 대응되는 경우가 생긴다. 예를 들어 변환된 픽셀의 위치가 정수가 아닌 실수로 나와서 반올림을 하게 되면, 원래는 없었던 crack과 hole이 생겨버린다. (100,100)이 깔끔하게 (50,50)으로 대응되면 좋겠지만, (50.2, 50.8)로 대응되어 (50, 51)에 (100,100)에 저장되어 있던 intensity 값이 paste 돼버리면 크랙과 구멍이 생길 수 있게 되는 거다.
따라서 이러한 forward warping의 문제를 막고자 Inverse warping을 사용한다. 이건 결과 화면의 픽셀에서 원래 화면의 픽셀을 대응시켜서 intensity 값을 채운다. 이렇게 하면 대응되는 픽셀이 정수로 나누어지지 않아도 괜찮다. 예를 들어 결과 화면의 (50,50) 위치의 픽셀에 대응 시킬 intensity 값을 찾기 위해 inverse warping을 했는데 원래 화면의 (100.2, 99.5) 픽셀이 나왔다면, 원래 화면의 (100.2, 99.5) 주변 픽셀 값들을 가지고 interpolation(resample)한 intensity 값을 결과 화면 (50,50) 위치에 paste 시켜주면 된다.



[Image Rotation]

위 그림에서 볼 수 있듯 회전을 나타내는 행렬은 위와 같다. 기본 좌표계(원점이 좌측 하단에 존재)에서 CCW(반시계) 방향이 forward, CW(시계) 방향이 inverse warping이다. 하지만 컴퓨터에서의 좌표는 원점이 좌측 상단에 존재하기에 CCW 방향이 inverse warping, CW 방향이 forward warping이다. 위에서 언급한 이유로 인해 우리는 warping 할 때 inverse warping 방식을 사용해주어야 한다. 따라서 위의 행렬(빨간 동그라미 표시된)을 사용할 것이다.
이 image rotation을 해서 inverse warping으로 pixel 값을 채우는 과정을 한 단계씩 알아보자. original location x,y가 있고, 회전 후 location x_r, y_r이 있다고 하자. 그리고 여기선 새로운 이미지가 원본 이미지 보다 크기가 크며, 회전을 한다고 가정한다.
1. 일단 inverse warping 방식으로 x_r, y_r에 대응하는 original location의 위치를 계산한다.
2. 만약 위치의 값이 정수가 아닌 실수로 나왔다면 주변 픽셀의 값들을 interpolation 한다.
3. 그렇게 해서 얻은 픽셀의 intensity 값을 x_r, y_r 픽셀 값에 붙여 넣는다.

위에서 보다시피 회전을 하면 화면상 더 큰 공간이 필요해진다. 따라서 100+a 크기를 가진 배열이 정확히 얼만큼의 크기를 가지는지 계산해주어야 한다.
[Ex1) Image Stitching using Affine Transformation]

Image stitching이란 여러 이미지를 하나의 큰 이미지로 결합하는 과정이다. 예를 들어 스마트폰 카메라의 파노라마 기능이라 생각하면 쉽다. 여기에는 affine transformation을 사용하여 두 이미지 I1, I2 간 관계를 모델링하고 두 이미지를 병합한다.
1. Estimate the affine transformation
affine transformation의 행렬을 구하는 방법을 알아보자.
우선 affine transformation을 행렬 연산으로 표시하면 다음과 같다.

그리고 이걸 다른 방식으로 표현하면 이렇게 표현할 수도 있다.

행렬로 linear equation을 표현한 것인데 affine transformation에는 매개변수 a,b,c,d,e,f 총 6개의 미지수가 있다. 6개의 미지수가 있을 때는 최소 6개의 식이 있어야 해답을 구할 수 있다. 근데 지금 방정식은 2개밖에 없기에 a,b,c,d,e,f 를 구하기 불충분하다. 따라서 두 이미지(원본, 변환 후 이미지)에서 3개 이상의 대응점(대응점 하나 당 2개의 식, 총 6개의 식이 나옴)을 이용해서 affine transformation 행렬을 추정해야한다. 이를 행렬로 표현하면 다음과 같다.
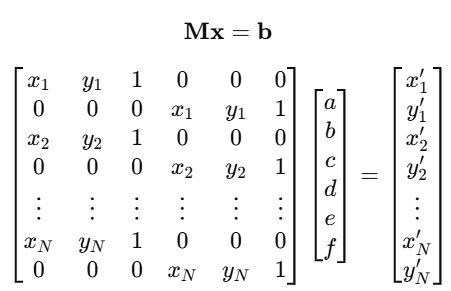
이 식을 풀기 위해서 Least Squares Method를 사용할 것이다. 그 이유는 현재 식이 x 기준으로 over-determined system이기 때문인데, 지금처럼 미지수보다 방정식 수가 더 많을 때 모든 경우에서 만나는 한 점이 있는 golden cross가 존재하지 않는 이상 |Mx-b|^2 값을 최소화하는 방식으로 풀어 최적의 변환 행렬을 추정할 수 있다.

2. Merge two images (I2 to I1)
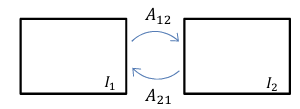
이미지 I2를 이미지 I1에 맞추기 위해, affine transformation A21을 이용해서 I2의 코너 좌표 p1,p2,p3,p4를 계산해야한다. 이걸 계산해주어야 최종 이미지 I_F의 크기를 결정할 수 있다. I1의 기존 코너 위치는 고정을 하고, I2의 코너 점들을 affine transformation 을 사용해서 I1의 좌표계로 변환한다. 그리고 반환된 4개의 좌표 p1,p2,p3,p4를 기반으로 최종 이미지의 크기를 설정한다.
하지만 앞서 말했듯이 image warping을 할 때 forward warping을 하면 crack과 hole이 생기는 문제가 발생하므로 inverse warping을 사용해줄 것이다. I2 -> I1으로 warp 하는 것에서의 forward warping은 A21다. 따라서 inverse warping인 A12를 사용해서 I2를 I1의 좌표 공간에 매핑시켜줄 것이다.

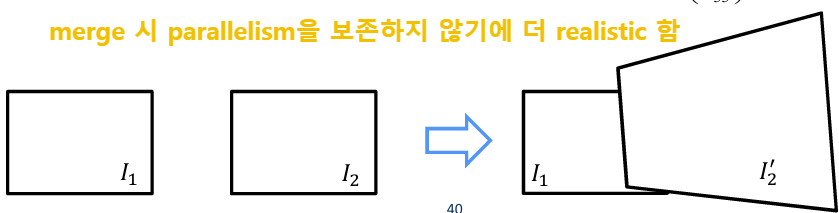
이렇게 inverse warping으로 merge를 하면 두 이미지가 겹치는 부분이 있을 수 있는데, 이때는 특정 공식에 맞춰 blending을 하면 된다. blending 식은 다음과 같다.

[Ex2) Image Stitching using Projective Transformation]
Ex1과 반대로 affine이 아닌 Projective Transformation을 이용한 image stitching에 대해 알아보자. 두 이미지 I1, I2를 정렬하는데 사용하는 transformation 행렬을 구하는 방식이 달라진다. 이때 사용하는 행렬은 homography matrix다. projective transformation은 두 이미지가 서로 다른 perspective에서 촬영된 경우, 하나의 이미지 좌표계를 다른 이미지 좌표계로 맞추는데 사용된다.
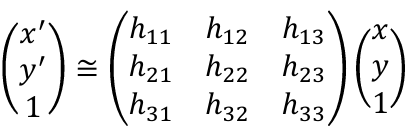
projective transfomation의 DoF는 8이므로 미지수가 8개인 방정식으로 취급되어, 최소 4쌍의 대응점(8개의 연립 방정식)이 필요하다. 위 행렬식을 변형하여 linear equation system으로 나타내면 다음과 같다.

그런데 위 식을 풀 때 Mx=0 형식이기에 x=0이라는 trivial solution이 존재한다. 하지만 이걸 원하는 것이 아니기 때문에 고유값과 고유벡터를 사용해서 값을 구해야 한다. 고유값과 고유벡터를 추정하기 위해 SVD(Singular Vector Decomposition) 을 사용한다. 행렬 M에 SVD를 적용해서 9개의 고유값과 고유벡터를 구하고, 크기가 가장 작은 고유값의 고유벡터를 정답으로 선택한다.
📝 ETC
* Super-resolution(SR): 저해상도 화면에 interpolation을 딥러닝 버전으로 적용해서 화질을 개선한 것
* harmonic theory: linear, NN, Cubic interpolation처럼 주변 값들을 가지고 값을 추정하는 것
❓ Question
1. 대비 ✅
intensity의 분산이 크면 대비가 큰 게 직관적으로 이해가 되지 않음
=> 대비가 높은 것은 이미지 안에서 명확한 차이를 보이는 것을 말한다. 즉 밝은 부분은 더 밝고, 어두운 부분은 더 어두운 것이다. 밝기의 분산이 크다는 건 픽셀 값들이 서로 멀리 퍼져 있다는 의미인데, 이미지에 밝은 부분과 어두운 부분이 뚜렷하게 존재한다는 것이다. 극단적으로 125-130 사이의 intensity 값들로만 이루어진 이미지를 생각하면, 이미지의 모든 부분이 전체적으로 밝기가 비슷하니 뭐가 뚜렷하게 드러나지 않을 것이다.
2. Uniform quantization ✅
여기서 uniform의 의미?
=> 일정한 간격으로 데이터를 구분하는 것. 즉, 전체 범위를 동일한 크기의 구간으로 나누는 것을 의미한다.
3. image의 size를 줄일 때의 pixel 크기
50x50의 이미지에 만약 픽셀 개수가 2500개. 여기서 이미지의 크기를 10x10으로 줄이는데 픽셀 개수를 2500개로 유지할 수 있는지? 그렇게 됐을 때 각 픽셀의 size는 어떻게 되는지? pixel의 크기는 변할 수 있는 것인가?

이건 그러면 픽셀의 크기가 커졌다라고 표현할 수 있는 건가? 진짜로 픽셀의 개수가 줄어든 것이라고 표현하는지 아니면, 픽셀의 개수는 그대로인데 효과가 그렇다는 것인지..
4. General interpolation form을 적용할 때 R 함수를 적용 시 정규화를 해서 그에 맞게 적용하는 건가?
5. homogenous coord에서 w 값을 x, y 값에 따라 배율 변환하는 것의 의미는?✅
=> 그래픽스 시간에 배운 내용에서 3D에서의 homogenous coord (x,y,z,w)와 2D에서의 homogenous coord (x,y,w) 헷갈렸다. z도 깊이(원근?)을 나타내는 정보고 w도 비슷한 것이라고 생각해서 이 둘의 정확한 역할이 헷갈렸다.
- 2D homogenous : w 값 하나만으로 "깊이감"을 표현하고 조정하는 것. 여기선 실제 깊이 값은 없고 w로 원근법을 모사하여 x,y 위치를 나타낸다.
- 3D homogenous : z로 깊이를 따로 표현하지만, 원근 투영할 때 z 깊이와 x, y 위치 정보를 w 값으로 보정을 하는 것이다.
6. 회전 방향 측정 방법✅
=> 기준이 되는 좌표축을 따라 양의 각도(+)와 음의 각도(-)로 구분. 회전 후 점의 위치가 이동했는데 x가 증가하고 y가 감소했다면 시계 방향, x가 감소하고 y가 증가했다면 반시계 방향이다.
※ 강의, 자료 출처
민동보 교수님. "Open Software Project." 이화여자대학교, 2023.
'인공지능 > 컴퓨터비전 기초' 카테고리의 다른 글
| [Open SW Project] OpenCV_tutorial (0) | 2025.01.24 |
|---|---|
| [Open SW Project] Lec01_Fundamentals (0) | 2025.01.19 |
| [Open SW Project] Lec00_Introduction (0) | 2025.01.18 |



